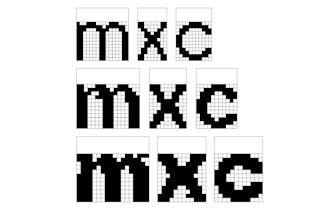Documentation
Visual was born at a workshop at the end of October (2010), but spiritually is a double Gemini – full of hot takes and internal contradictions. Its exterior is systematic, adhering to a strict grid – rendering an appearance of re-booting back to an era of bitmap fonts – while its counters are organic – hacking the rules of the rest of its system. A fitting take on a raster font as today’s screens (obviously) no longer require the coarseness that Zuzana Licko had to work within for the first generations of personal computers (1985, Oakland¹), or perhaps an even earlier system from Giuseppe Salviati, who developed templates for cross stitch embroidery (1567, La Vera Perfettione del Disegno di varie sorti di recami²). Thus it is fitting that a (semi) pixel family released in 2023 is not limited to the constraints which defined previous eras. In Visual, the gradation of pixels follow in the same steps in each of its styles – the weight is increased through the width of the character, and the inner curves which form its counters enable the letterforms to become optically balanced.
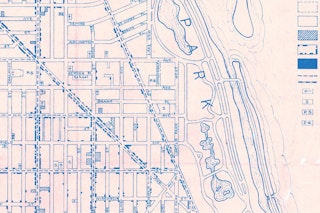
A simple prompt resulted in a nuanced output – create something typographically new inspired by topographic maps, the goal to work through: ‘freely connecting the disciplines of typography and topography.’ The workshop resulted in a single weight and a poster after a 1-week workshop led by Áron Jancsó, Ján Filípek, and Ondrej Jób. In the initial steps of the workshop Jan Novák surfed the internet from Báhoň, SK to Chicago, USA – to catch a birds-eye view, of a zoo. Inspired by overlapping geometric and natural elements in a map of Lincoln Park Zoo, Jan developed a typeface inspired by these maps – not immediately sketched on screen, but developed first from drawings on paper. No longer limited by the historical design problem of adhering to a lo-res grid due to production constraints, the (then) advanced technology of Fontlab Studio 5.1 enabled Jan to create a typeface which had the characteristics of a pixel font but the dynamism of something new.
Read more →
In 2022, Jan returned to the project, expanding the typeface into a family with 6 cuts. During the refinement process, shapes which previously existed in a purely geometric perspective were optically condensed to behave in a more functional way. Operating as a neo-grotesque while emulating Gameboy energy.
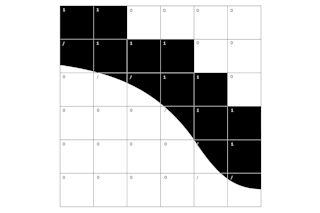
ZOOming out creates a different kind of perspective, the edges blur and become simplified. Despite its aliased appearance, Visual functions quite well for text setting, as the rough edges are softened when viewed from a reading distance – not unlike another famous topographic-to-intergalactic moment (coincidentally also featuring an overview of Chicago), the Ray and Charles Eames film comissioned by IBM: Powers of Ten: A Film Dealing with the Relative Size of Things in the Universe and the Effect of Adding Another Zero³. A timeless reminder that we are floating through a rock in space (aka Earth) – perhaps it would be ideal to spec your glyphs from an elevated perspective, and then go outside.
1 Zuzana Licko, Oakland, 1985. Digital typeface, Emigre Inc. MoMA Collection
2 Giuseppe Salviati, La Vera Perfettione del Disegno di varie sorti di recami, 1567. Woodcut, Giovanni Ostaus. The Metropolitan Museum of Art Collection
3 Ray and Charles Eames, Powers of Ten™, 1977. Film, Eames Office.
Technical Information:
Design: Jan Novák
Design assistance: Přemysl Zajíček, Ishar Hawkins, Rebekka Hausmann
Classification: Semi-Pixel Geometric Sans
Cuts: 6
Mastering: Michele Patanè
Cover artwork: Rebekka Hausmann
First sketch: 2010
Released: 2023
Latest update: 09/2023
OpenType Features:
- aalt
- Access All Alternates
- calt
- Contextual Alternates
- case
- Case Sensitive Forms
- dnom
- Denominator
- frac
- Fractions
- locl
- Localized Forms
- numr
- Numerator
- ordn
- Ordinals
- sinf
- Scientific Inferiors
- subs
- Subscript
- sups
- Superscript
Supported Languages:
Afrikaans, Albanian, Asu (Tanzania), Basque, Bemba (Zambia), Bena (Tanzania), Breton, Catalan, Chiga, Cornish, Croatian, Czech, Danish, Dutch, Embu, English, Esperanto, Estonian, Faroese, Filipino, Finnish, French, Friulian, Galician, Ganda, German, Gusii, Hungarian, Icelandic, Inari Sami, Indonesian, Irish, Italian, Jola-Fonyi, Kabuverdianu, Kalaallisut, Kalenjin, Kamba (Kenya), Kikuyu, Kinyarwanda, Latvian, Lithuanian, Lower Sorbian, Luo (Kenya and Tanzania), Luxembourgish, Luyia, Machame, Makhuwa-Meetto, Makonde, Malagasy, Maltese, Manx, Meru, Morisyen, North Ndebele, Northern Sami, Norwegian Bokmål, Norwegian Nynorsk, Nyankole, Oromo, Polish, Portuguese, Quechua, Romanian, Romansh, Rombo, Rundi, Rwa, Samburu, Sango, Sangu (Tanzania), Scottish Gaelic, Sena, Serbian, Shambala, Shona, Slovak, Slovenian, Soga, Somali, Spanish, Swahili (macrolanguage), Swedish, Swiss German, Taita, Teso, Turkish, Upper Sorbian, Uzbek, Volapük, Vunjo, Walser, Welsh, Western Frisian, Zulu
Buy Visual Family
Single Styles
Buying guide
We offer the possibility of buying individual styles as well as complete families. The price shown is the cost of our most basic licence. Further licencing options are available during the checkout process.
Character Overview
- Character name
- Unicode Decimal
- 65
- Unicode Hex
- 41
- HTML Entity (Hex)
- A
Uppercase
- 65A
- 66B
- 67C
- 68D
- 69E
- 70F
- 71G
- 72H
- 73I
- 74J
- 75K
- 76L
- 77M
- 78N
- 79O
- 80P
- 81Q
- 82R
- 83S
- 84T
- 85U
- 86V
- 87W
- 88X
- 89Y
- 90Z
Lowercase
- 97a
- 98b
- 99c
- 100d
- 101e
- 102f
- 103g
- 104h
- 105i
- 106j
- 107k
- 108l
- 109m
- 110n
- 111o
- 112p
- 113q
- 114r
- 115s
- 116t
- 117u
- 118v
- 119w
- 120x
- 121y
- 122z
Uppercase Accents
- 193Á
- 258Ă
- 194Â
- 196Ä
- 192À
- 256Ā
- 260Ą
- 197Å
- 195Ã
- 198Æ
- 262Ć
- 268Č
- 199Ç
- 264Ĉ
- 266Ċ
- 208Ð
- 270Ď
- 272Đ
- 201É
- 276Ĕ
- 282Ě
- 202Ê
- 203Ë
- 278Ė
- 200È
- 274Ē
- 280Ę
- 7868Ẽ
- 286Ğ
- 284Ĝ
- 290Ģ
- 288Ġ
- 294Ħ
- 292Ĥ
- 7716Ḥ
- 306IJ
- 205Í
- 206Î
- 207Ï
- 304İ
- 204Ì
- 298Ī
- 302Į
- 296Ĩ
- 308Ĵ
- 310Ķ
- 313Ĺ
- 317Ľ
- 315Ļ
- 7734Ḷ
- 321Ł
- 323Ń
- 327Ň
- 325Ņ
- 330Ŋ
- 209Ñ
- 211Ó
- 334Ŏ
- 212Ô
- 214Ö
- 210Ò
- 336Ő
- 332Ō
- 216Ø
- 213Õ
- 338Œ
- 222Þ
- 340Ŕ
- 344Ř
- 346Ś
- 352Š
- 350Ş
- 348Ŝ
- 536Ș
- 7838ẞ
- 358Ŧ
- 356Ť
- 354Ţ
- 538Ț
- 218Ú
- 364Ŭ
- 219Û
- 220Ü
- 217Ù
- 368Ű
- 362Ū
- 370Ų
- 366Ů
- 360Ũ
- 7810Ẃ
- 372Ŵ
- 7812Ẅ
- 7808Ẁ
- 221Ý
- 374Ŷ
- 376Ÿ
- 7922Ỳ
- 377Ź
- 381Ž
- 379Ż
Lowercase Accents
- 225á
- 259ă
- 226â
- 228ä
- 224à
- 257ā
- 261ą
- 229å
- 227ã
- 230æ
- 263ć
- 269č
- 231ç
- 265ĉ
- 267ċ
- 240ð
- 271ď
- 273đ
- 233é
- 277ĕ
- 283ě
- 234ê
- 235ë
- 279ė
- 232è
- 275ē
- 281ę
- 7869ẽ
- 287ğ
- 285ĝ
- 291ģ
- 289ġ
- 295ħ
- 293ĥ
- 7717ḥ
- 305ı
- 237í
- 238î
- 239ï
- 236ì
- 307ij
- 299ī
- 303į
- 297ĩ
- 309ĵ
- 311ķ
- 312ĸ
- 314ĺ
- 318ľ
- 316ļ
- 7735ḷ
- 322ł
- 324ń
- 329ʼn
- 328ň
- 326ņ
- 331ŋ
- 241ñ
- 243ó
- 335ŏ
- 244ô
- 246ö
- 242ò
- 337ő
- 333ō
- 248ø
- 245õ
- 339œ
- 254þ
- 341ŕ
- 345ř
- 347ś
- 353š
- 351ş
- 349ŝ
- 537ș
- 223ß
- 359ŧ
- 357ť
- 355ţ
- 539ț
- 250ú
- 365ŭ
- 251û
- 252ü
- 249ù
- 369ű
- 363ū
- 371ų
- 367ů
- 361ũ
- 7811ẃ
- 373ŵ
- 7813ẅ
- 7809ẁ
- 253ý
- 375ŷ
- 255ÿ
- 7923ỳ
- 378ź
- 382ž
- 380ż
Numerals
- 480
- 491
- 502
- 513
- 524
- 535
- 546
- 557
- 568
- 579
Dingbat Numerals
- 9471⓿
- 10102❶
- 10103❷
- 10104❸
- 10105❹
- 10106❺
- 10107❻
- 10108❼
- 10109❽
- 10110❾
Currency & Math
- 8383₿
- 162¢
- 164¤
- 36$
- 8364€
- 8356₤
- 8378₺
- 163£
- 165¥
- 8901⋅
- 43+
- 8722−
- 215×
- 247÷
- 61=
- 8800≠
- 62>
- 60<
- 8805≥
- 8804≤
- 177±
- 8776≈
- 126~
- 172¬
- 94^
- 8734∞
- 8709∅
- 8747∫
- 960π
- 8710∆
- 8486Ω
- 181µ
- 8719∏
- 8721∑
- 8730√
- 8706∂
- 37%
- 8240‰
Superscript
- 8304⁰
- 185¹
- 178²
- 179³
- 8308⁴
- 8309⁵
- 8310⁶
- 8311⁷
- 8312⁸
- 8313⁹
Subscript
- 8320₀
- 8321₁
- 8322₂
- 8323₃
- 8324₄
- 8325₅
- 8326₆
- 8327₇
- 8328₈
- 8329₉
Ordinals
- 170ª
- 186º
Punctuation & Symbols
- 46.
- 44,
- 58:
- 59;
- 8230…
- 33!
- 161¡
- 63?
- 191¿
- 183·
- 8226•
- 35#
- 47/
- 92\
- 40(
- 41)
- 123{
- 125}
- 91[
- 93]
- 45-
- 8211–
- 8212—
- 95_
- 8218‚
- 8222„
- 8220“
- 8221”
- 8216‘
- 8217’
- 8249‹
- 8250›
- 34"
- 39'
- 9679●
- 9675○
- 9674◊
- 9632■
- 9633□
- 64@
- 38&
- 182¶
- 167§
- 169©
- 174®
- 8471℗
- 8482™
- 176°
- 8242′
- 8243″
- 124|
- 166¦
- 8224†
- 8225‡
- 65533�
Fraction
- 189½
- 8585↉
- 8531⅓
- 8532⅔
- 188¼
- 190¾
- 8533⅕
- 8534⅖
- 8535⅗
- 8536⅘
- 8537⅙
- 8538⅚
- 8528⅐
- 8539⅛
- 8540⅜
- 8541⅝
- 8542⅞
- 8529⅑
- 8530⅒
Arrows
- 8593↑
- 8594→
- 8595↓
- 8592←
- 8599↗
- 8600↘
- 8601↙
- 8598↖
- 8596↔
- 8597↕